线性的数据结构
张桄玮
郑州一中(Legacy)
本节概述
回顾: 程序=算法+数据结构
- 拿着说明书操作某些东西
今天上午: 基本的数据结构
- 链表(到处都是)
- 栈
- 队列
遵循的逻辑
- 先手写
- 然后再使用STL库写
链表
考虑如下场景

思考: 什么是链表?
- 那个把一堆东西串成一个链的东西
神经的定义说: 链表是
- 什么都没有算是一个链表
- 一个链表, 它的下一个元素指向一个链表的东西是链表
实际上是链表的递归定义(DP的时候很有用)
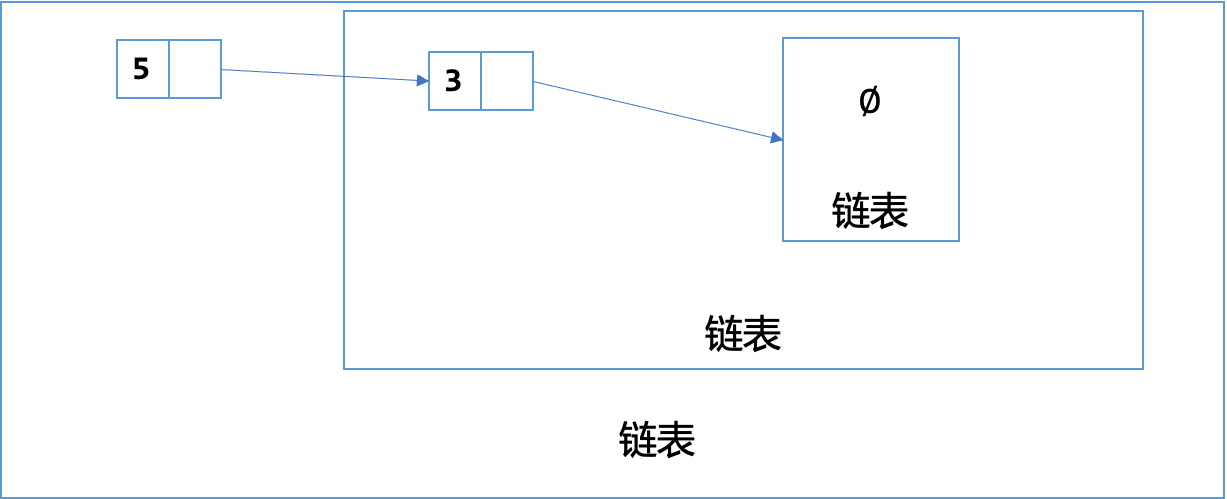
如何表示同一类的东西?
想法1: 把它们放到 “隔间” 里面, 对隔间(内存池)编号.
- 单开一个数组, \(nxt[i]:=第i个元素的下一个是第几号?\)
很好的想法!
问题: 如果下一个没有了, 怎么办?
- 设置一个正常数据不可出现的特殊值(如-1)
- 额外开设一个 \(hasnxt[i]:=i是否有下一个元素\)
疑问: 这不还是数组吗?
- 答案: 这样更快!
- 计算机内存就是一个大数组 \(2^{64}\) 的寻址空间
结构的定义之一
int head, // 这个链表的头是哪个节点
idx, // 当前链表里面有几个节点
val[MAXN], // val[i]:=编号为i的格子里的数据
nxt[MAXN]; // nxt[i]:=编号为i的格子的下一个格子编号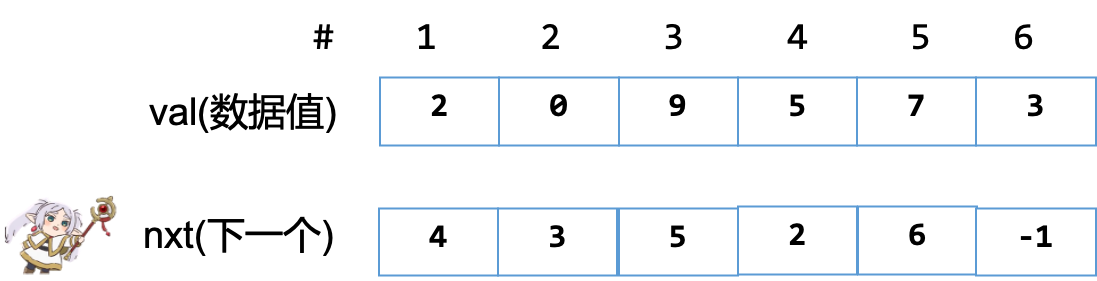
快速问答: 构成的链表是什么?
- \(2 \to 5 \to 0 \to 9 \to 7 \to 3\)
操作A: 初始化(init)
初始状态: 链表中没有任何元素
维护一个数据结构 = 让所有的数据和指针恢复正确的位置
- 没有数据 \(\to\) 头部不存在(用-1)代替
- 当前分配的内存池还没有用(有0个节点)
操作B: 在头部添加一个节点(prepend)
哪些需要改变?
- 新插入了节点, 顶多新插入的和当前的头需要改变
- 链表可以看做递归的结构
操作B2: 在内存池的第 \(k\) 位置后面增加一个节点(add)
哪些需要改变?
- 插入节点的
nxt - 新建节点的
nxt - 当前的内存池的使用的top
操作C: 删除内存池的节点 \(k\) 后面的元素
- 直接修改当前节点的
next指向next的nextnxt[k] = nxt[nxt[k]];
- 问题: 当前使用内存池
idx要idx-=1吗?
- 不用! 分配出去就不管了…
单链表插入和删除的思考
为什么我们总是说插入/删除格子的后面的元素?
- 如果要插入/删除格子的第 \(k\) 个元素, 怎么做?
需要知道我前面是谁
- 但是我只记录了后面的信息, 就需要从头把链表扫描一遍!
解决方法
- 可以维护两个结构
- \(nxt[i]:=第i个格子的下一个是谁\)
- \(prv[i]:=第i个格子的前一个是谁\)
- 好处: 可以之间删除当前节点 / 坏处: 维护的节点多了
双向链表介绍
结构
int val[N], // val[i]:=表示结点i存储的数值
prv[N], // prv[i]:=节点i的前一个节点是哪个节点
nxt[N], // nxt[i]:=节点i的下一个节点是哪个节点
idx; // 内存池现在用了几个节点问题: 怎么初始化?
- 第一个节点的左边
- 第二个节点的右边
是不是可以加一个 “空白” 节点, 表示这是结束?
- 在头部和尾部分别加入一个节点作为空白节点
- 甚至可以把第一个的prv和最后一个的nxt都指向这个空白节点
- 循环起来了!
操作A: 初始化(dll-init)
- 让0,1节点做开头和结尾的空白节点
操作B: 在内存池 \(k\) 的位置右边插入一个节点(dll-add)
画一个草图
- 注意边界情况: 插入第一个/最后一个
操作C: 删除内存池 \(k\) 的节点(dll-remove)
还是, 画一个草图
- 注意边界情况: 删除第一个/最后一个
//删除内存池里面编号为k的点
void remove(int k) {
//就是将k的左端点和右端点相互连接
prv[nxt[k]] = prv[k];
nxt[prv[k]] = nxt[k];
}- 奇怪的边界情况都消失了, 为什么?
- 我们规定死了0号节点永远是头!
使用struct管理数组元素
其中
prv[i]变为了dlls[i].prv, 看上去变得清楚一些, 但是打的字长一点
习题: P1160 队列安排
指针简介
回顾刚刚的内存池带来的 “隐患”(不太可能在OI发生, 但是提一下)
- 我真的不想让已经删除的节点占据空间, 怎么办?
- 维护两个链表, 一个是
active, 一个是free - 添加一个节点=从
free里面薅一个加到active里面 - 移除一个节点=从
active里面把它断掉加到free里面
- 维护两个链表, 一个是
- 如果我移除了第 \(k\) 个节点之后,
不小心又移除了怎么办? (double free)
- 肯定是你的逻辑写错了!
- 上面的写法: 有可能free一个已经被占用的列表项 \(\to\) 程序出现非预期的行为
马上: 介绍指针
什么是指针
关注变量的: 类型/里面存的值/地址
变量存在哪? 内存的 “单元” 里面
- 有门牌号: 用&获取其值, 类型是
Type *(pointer to type)
指针: A pointer is a variable that contains the address of a variable
- 指针解引用: 把当前变量的值当做地址, 操纵在那个地址的变量的值
- 在lvalue处会使用*表示指针解引用, 其效果就和直接操纵变量一样
指针与数组
- 在表达式中, 数组的名字和它第一个元素的地址是同义词
- 但是数组名不是变量, 数组和指针是两个不同的类别
- 推荐二周目学习C语言观看
- 这甚至还不是C++! 谁知道C++里面有什么诡异的特性…
- 但是用好大部分就好了…
结构体与指针
用指针写一个循环链表
链表结构体
操作A: 初始化(cdll-init)
操作B: 前插一个值(cdll-prepend)
操作C: 删除某一个节点(cdll-del)
检查: 输出链表的形态
void __attribute__((unused)) inspect_tnode(TSKLST *bd){
task_t *start = &bd->dummy;
// Log("%p\n", start);
int count = 0;
start = start->nxt;
while(start != &bd->dummy){
panic_on(start->prv->nxt != start, "Did not maintain the llist well.");
printf("[%s]->", start->name);
count++;
start = start->nxt;
}
printf("NIL\n");
panic_on(count != bd->nr_node, "Did not maintain size well.");
}平时调试的时候保护自己不受伤害
panic_on是啥?- 在
xxx的条件下恐慌(退出程序)
- 在
- 为什么? 程序在不对的状态的时候今早退出!!
- 越早暴露问题, 就越好调试
怎么实现?
空指针解引用的时候会引发SIGSEGV(段错误)
- 正式交上去的时候不用加, 有一定几率
程序靠bug通过测试 - 但是开O2就有可能出问题了…为什么?
STL中的链表: list
参看stl-list.cpp
练习链表
- P1996 约瑟夫问题
- Uva11988 破碎的键盘
- Uva12657
如果有2个或者多个链表, 将他们组成结构体是个好主意
栈
栈是后进先出的数据结构
栈: stack: 一叠/堆叠
生活中的实例
- 羽毛球桶
模拟方式: 使用数组, 追踪栈顶是谁
练习: B3614 栈
你们可能会的
- P1739 表达式括号匹配
Uva 514 铁轨
题目大意: 判定一个序列是否可以由栈构成另一个序列?
栈的操作:
- 只要输入还没有处理完
- 把某一长度的东西放进去, 然后反序输出
另一种观点
- 一步决策不是弹出就是再压一个东西进去
P1449 后缀表达式
- 这类似一道模拟题
P1175 表达式转换A
- 中缀表达式 \(\to\) 后缀表达式
词法分析: 简单(数字只有一位!)
总体思路:
- 先抑制符号的输出, 等到两个操作数输出完了后输出符号
- 当前字符0-9, 直接输出
- 多步运算, 后面来的先算: 使用栈
P1175 表达式转换(继续)B
第一个问题: 优先级
- 最先算乘方, 先算乘除, 再算加减
- 见到高优先级进来就等一等(先算这个子部分); 低优先级就一直弹出到和当前的优先级持平的位置
- 甚至适用括号
- 括号的优先级是0.
第二个问题: 结合律
+-*/是左结合的: \(2+3+4=((2+3)+4)\)- 乘方是右结合的: \(2^{3^4}={2^{(3^4)}}\neq2^{12}\).
- 特殊: 设定最高的优先级;
当
^与^相同的时候要入栈
P1175 表达式转换(继续)C
细节: 我怎么输出?
- 还是因为这里只有0-9, 因此不能输出大于10的数. 如果是就是符号
好麻烦!
- 实际上这模拟的是 LR语法分析算法.
有一类稍微简单一点的, 考虑表达式的递归特性
P1175 表达式转换(继续)D
每次选出优先级最低的那个节点, 并且在两边分裂!
- 大学: ~2hr就可以写完的 编程实验的一部分.
练习题
- P1981 表达式括号匹配
将递归的过程改写为非递归
练习: 将下面的函数改写为非递归的形式
void hanoi(int n, char from, char to, char via) {
if (n == 1) printf("%c -> %c\n", from, to);
else {
hanoi(n - 1, from, via, to);
hanoi(1, from, to, via);
hanoi(n - 1, via, to, from);
}
return;
}- 这样你们就理解了递归的语义
STL中的stack
只能访问最顶上的元素
push和pop
- 文档
队列
队列是先进先出的数据结构
使用链表模拟队列:
头 \(\to\) 尾
- 插入: 在头部插入一个
- 移除: 在尾部移除
练习: B3616
循环队列
如果要用数组模拟
- 开两个指针, 头和尾
- 如果进一个出一个, 进一个出一个, 一会儿就会好像”满了”
处理办法:
- tail满了的时候从头来
- head和tail相遇才是真的满了
操作A: 结构定义(cqueue-init)
- front: 队头的那个元素, rear: 队尾的那个元素后面的那个空位
- 一个模队列长度的运算系统
属性B: 大小, 长度(cqueue-size)
属性C: 推入, 弹出
bool push(int e){
if((rear+1)%NR_DAT==front) return false; // full!
data[rear] = e;
rear = (rear+1)%NR_DAT;
return true;
}
bool pop(int &e){
// ^ Using reference will make the argument change
// equivalent to int *eptr
if(front == rear) return false;
e = data[front];
// *etpr = data[front];
front = (front + 1)%NR_DAT;
return true;
}STL的queue
尾部入队, 头部出队
双端队列
- 要求两边既可以插入, 也可以删除
链表: 这我熟!
数组: (长度为 \(n\) )不考虑溢出的话就是一个带着head和tail的栈
INC(x) -> (x+1)%NR_DATDEC(X) -> (x-1+NR_DAT)%NR_DAT
STL: deque(读音deck, /dēˈkyo͞o/是dequeue, 出队的意思)
- 马上介绍STL的时候讲解
STL中双端队列deque
内部实现还是使用的数组
单调队列与滑动窗口
求一个窗口里面的最大值/最小值
| 最小值 | 最大值 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| \([1\) | 3 | \(-1]\) | -3 | 5 | 3 | 6 | 7 | -1 | 3 |
| 1 | \([3\) | -1 | \(-3]\) | 5 | 3 | 6 | 7 | -3 | 3 |
| 1 | 3 | \([-1\) | -3 | \(5]\) | 3 | 6 | 7 | -3 | 5 |
| 1 | 3 | -1 | \([-3\) | 5 | \(3]\) | 6 | 7 | -3 | 5 |
| 1 | 3 | -1 | -3 | \([5\) | 3 | \(6]\) | 7 | 3 | 6 |
| 1 | 3 | -1 | -3 | 5 | \([3\) | 6 | \(7]\) | 3 | 7 |
考虑食堂打饭的情景
- 打饭的时候, 总是希望前面的同学比自己矮, 就可以看到菜
- 维护队伍的单调性
- 窗口大小有限! 有时候大小超限需要把队头弹掉
核心操作
- 掐头: 队头的元素不在窗口的范围内就从队头弹出
- 去尾: 维持队列的单调性(既可以进又可以出)
P1886 滑动窗口/单调队列
最小的队列如上所示;
最大的队列就是把某个符号反过来.
- 问题: 把哪个符号反过来?
练习: P1440 求 \(m\) 区间的最小值